En matemáticas , el teorema de los cuatro colores establece que en cualquier partición de un plan en regiones contiguas, que produce una figura llamada mapa , no se necesitan más de cuatro colores para colorear las regiones del mapa de forma que no haya dos regiones adyacentes del mismo color. Dos regiones se llaman adyacentes si comparten una frontera común que no sea una esquina, donde las esquinas son los puntos compartidos por tres o más regiones. Por ejemplo, en el mapa de los Estados Unidos de América , Utah y Arizonason adyacentes, pero Utah y Nuevo México, Que sólo comparten un punto que también pertenece a Arizona y Colorado , no lo son.
A pesar de la motivación de colorear los mapas políticos de los países, la cartografía no está particularmente interesada en el teorema. Según un artículo del historiador de matemáticas Kenneth May, "son raros los mapas que utilizan sólo cuatro colores, y los que lo hacen en general sólo necesitan tres. Los libros de cartografía e historia de la cartografía no mencionan la propiedad de los cuatro colores ".
En los mapas más simples tres colores son suficientes, pero en algunos casos se necesita un cuarto color adicional para algunos mapas, tales como aquellos en los que una región está rodeada por un número impar de otras regiones que se tocan en un ciclo. El teorema de los cinco colores , que tiene una corta demostración elemental, establece que cinco colores son suficientes para colorear un mapa y se demostró el siglo XIX; en cambio, demostró que cuatro colores son suficientes resultó ser significativamente más difícil. Ha habido una serie de demostraciones y contraejemplos falsas desde el primer enunciado del teorema de los cuatro colores en 1852.
El teorema de los cuatro colores fue demostrado en 1976 por Kenneth Appel y Wolfgang Haken. Fue el primer teorema importante al ser demostrado mediante un ordenador. El enfoque de Appel y Haken comenzó mostrando que hay un conjunto particular de 1.936 mapas, cada uno de los cuales no puede formar parte de un contraejemplo de tamaño más pequeño por el teorema de los cuatro colores. Appel y Haken utilizaron un programa informático especialmente diseñado para confirmar que cada uno de estos mapas tenían la propiedad de poder ser coloreados con cuatro colores. Además, cualquier mapa (independientemente de si se trata de un contraejemplo o no) debe tener una porción que se parece a uno de esos 1.936 mapas. Demostrar esto requirió cientos de páginas de análisis a mano. Appel y Haken llegaron a la conclusión de que no existían contraejemplos más pequeños, ya que cualquiera debería contener, pero en cambio no contiene, uno de estos 1.936 mapas. Esta contradicción significa que no hay en realidad ningún contraejemplo y que, por tanto, el teorema es cierto. Inicialmente, su demostración no fue aceptada por todos los matemáticos, porque la demostración asistida por ordenador era imposible de comprobar a mano por un humano. Desde entonces, la prueba ha ganado más aceptación, aunque persisten algunas dudas.
Para disipar las dudas restantes sobre la demostración de Appel-Haken, en 1997 Robertson, Sanders, Seymour y Thomas publicaron una demostración más sencilla que utilizaba las mismas ideas y que seguía basándose en los ordenadores. Además, en 2005 Georges Gonthier demostró el teorema utilizando software de demostración de teoremas de propósito general.
Formulación precisa del teoremade los 4 colores
El teorema de los cuatro colores se puede enunciar de manera intuitiva como
|
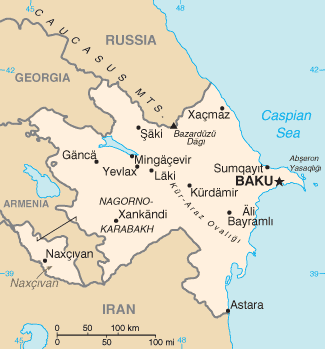
Ejemplo de un mapa del Azerbaiyán con regiones no contiguas
Para que este enunciado intuitivo del teorema de los cuatro colores sea correcto, hay que interpretarlo adecuadamente. En primer lugar, todas las esquinas, puntos que pertenecen a tres o más países, deben ignorarse. Además, algunos mapas extraños (que por ejemplo utilicen regiones de área finita pero perímetro infinito) pueden requerir más de cuatro colores.
En segundo lugar, para el propósito del teorema cada "país" debe ser una región simplemente conexa , o contigua. En el mundo real, esto a menudo no es así (por ejemplo, Michigan y su península superior , Najicheván como parte del Azerbaiyán , y Kaliningrado como parte de Rusia no son contiguos). Como el territorio de un país en particular debe ser del mismo color, en estos casos cuatro colores pueden no ser suficientes. Por ejemplo, considérese un mapa simplificado:
En este mapa, las dos regiones marcadas A pertenecen a un mismo país, y deben ser del mismo color. Este mapa requiere por tanto cinco colores, ya que las dos regiones A juntas son contiguas a cuatro otras regiones, cada una de las cuales es contigua con el resto. Si A se compusiera de tres regiones, se podrían necesitar seis o más colores; de esta manera se pueden construir mapas que requieran un número arbitrariamente alto de colores. Una construcción similar se aplica también si se utiliza un solo color para todos los cuerpos de agua, como suele ser habitual en los mapas reales.
Una versión más fácil de enunciar el teorema utiliza la teoría de grafos . El conjunto de las regiones de un mapa se puede representar de manera más abstracta como un grafo no dirigido que tiene un vértice para cada región y una arista para cada par de regiones que comparten un segmento de frontera. Este grafo es plano (es importante tener en cuenta que estamos hablando de grafos que tienen algunas limitaciones sólo según el mapa del que provienen): se puede dibujar en el plano sin cruces colocando cada vértice en un emplazamiento escogido arbitrariamente dentro de la región a la que corresponde, y dibujando las aristas como curvas que conducen sin cruzar ninguna región desde el vértice interno en una región hasta un punto de la frontera compartida con otra región. Lo mismo es cierto en sentido contrario: a partir de cualquier grafo plano se puede dibujar un mapa. En la terminología de teoría de grafos, el teorema de los cuatro colores enuncia que los vértices de cualquier grafo plano se pueden colorear con cuatro colores como máximo, de manera que ninguna pareja de vértices adyacentes tengan el mismo color, o de manera más concisa:
|
O equivalentmente:
|
donde es el número cromático del grafo .
Historia del teorema de los 4 colores
Intentos de demostración iniciales
Augustus De Morgan
Ya en 1840, Möbius mencionó el problema en sus conferencias. La conjetura fue propuesta por primera vez el 23 de octubre de 1852, cuando Francis Guthrie, al tratar de colorear el mapa de los condados de Inglaterra, se dio cuenta de que sólo eran necesarios cuatro colores diferentes. En este momento, el hermano de Guthrie, Frederick, era un estudiante de Augustus De Morgan (el exsupervisor de Francis) en University College de Londres . Francis lo discutió con Frederick, quien luego llevó el problema a De Morgan (Francis Guthrie se graduó más adelante, en 1852, y luego se convirtió en profesor de matemáticas en Sudáfrica). Según De Morgan:
| « | (ángulos) Un alumno mío [Guthrie] me preguntó a día para darle una razón de un hecho que no sabía era un hecho - y no lo hacen todavía. Se dice que si una figura ser cualquier forma dividida y los compartimentos de color diferente para que figuras con cualquier parte de la línea límite común son de color diferente - cuatro colores pueden querían pero no más - el siguiente es el caso en el que se quieren cuatro colores. Consulta puede no una necesidad para cinco o más se inventó ... | (catalán) Uno de mis estudiantes [Guthrie] me ha pedido hoy de darle una razón a un hecho que yo no sabía que fuera un hecho -y que aún ahora no lo sé. Dice que si una figura sea dividida de cualquier forma y los compartimentos coloreados de un color diferente de tal manera que las figuras que compartan cualquier parte de frontera común sean de un color diferente, entonces se pueden necesitar cuatro colores, pero no más. Lo que sigue es su caso en el que se necesitan cuatro colores. Busca que no se pueda inventar una necesidad para cinco o más ... | » |
Extracto de la carta original de De Morgan a Hamilton sobre la conjetura de los cuatro colores (23 de octubre de 1852, Trinity College, Dublin)
"FG", quizás uno de los dos Guth, publicó la pregunta al Athenaeum , una revista londinense, en 1854, y De Morgan planteó la pregunta de nuevo a la misma revista en 1860. otra referencia publicada por Arthur Cayley a su vez acredita la conjetura a De Morgan.
Hubo varios intentos fallidos de demostrar el teorema. De Morgan creía que se desprendía de un hecho simple sobre cuatro regiones, aunque no creía que este hecho se pudiera derivar de hechos más elementales.
| « | (ángulos) Esto surge de la siguiente manera. Nunca necesitamos cuatro colores en un barrio a menos que haya cuatro condados, cada uno de los cuales tiene líneas de frontera en común con cada uno de los otros tres. Tal cosa no puede suceder con cuatro zonas menos que uno o más de ellos ser encerrado por el resto; y el color utilizado para el condado cerrado eres, por lo tanto puesto en libertad para continuar con. Ahora bien, este principio, que cuatro zonas que no pueden tener cada una frontera común con todos los otros tres sin cercado, ¿no, tenemos la plena convicción, capaz de demostración sobre nada más evidente y más elemental; debe presentarse como un postulado. | (catalán) Esto surge de la siguiente manera. Nunca necesitamos cuatro colores en un barrio salvo cuatro condados, cada uno de los cuales tiene fronteras en común con cada uno de los otros tres. Algo así no puede pasar con cuatro áreas a menos que una o más de ellas estén rodeadas por la reza; y el color utilizado para el condado cerrado es por tanto libre. Ahora bien, este principio, que cuatro zonas que no pueden tener cada una frontera común con todas las otras tres sin estar rodeadas, no es, estamos plenamente convencidos, capaz de ser demostrada a partir de nada más evidente y más elemental; se presentará como un postulado. | » |
| - Augustus De Morgan, La Filosofía del descubrimiento, los capítulos históricos y críticos. | |||
En 1879, Alfred Kempe ofreció una supuesta demostración, que fue ampliamente reconocida; en 1880, Peter Guthrie Tait ofreció otra. No fue hasta 1890 que Percy Heawood mostró que la demostración de Kempe era incorrecta, y en 1891 Julius Petersen mostró que la demostración de Tait también era incorrecta -cada demostración errónea permaneció pues indiscutida durante 11 años.
En 1890, además de mostrar los errores en la demostración de Kempe, Heawood demostró el teorema de los cinco colores y generalizó la conjetura de los cuatro colores a superficies arbitrarias.
En 1880, Tait mostró que el teorema de los cuatro colores es equivalente a la afirmación de que un cierto tipo de grafo (un grafo conexo, sin puentes, cúbico y de número cromático 4) debe ser no- plan .
En 1943, Hugo Hadwiger formuló la conjetura de Hadwiger, una generalización de largo alcance del problema de los cuatro colores que aún sigue sin resolverse.
Demostración por ordenador
Durante las décadas de 1960 y 1970, el matemático alemán Heinrich Heesch desarrolló métodos para utilizar ordenadores para buscar demostraciones. Cabe destacar que fue el primero en utilizar el método de descarga para demostrar el teorema, que resultó ser importante en la parte inevitable de la posterior demostración de Appel-Haken. También se estudió el concepto de reductibilidad y, junto con Ken Durre, se desarrolló una prueba de ordenador. Desafortunadamente, en este momento crítico, no pudo conseguir el tiempo de supercomputación necesario para continuar su trabajo.
Otros matemáticos continuaron a partir de sus métodos y de su enfoque de utilizar el ordenador. Mientras que otros grupos de matemáticos competían para conseguir demostraciones completas, Kenneth Appel y Wolfgang Haken, de la Universidad de Illinois anunciaron, el 21 de junio de 1976, que habían demostrado el teorema. Recibieron la asistencia de John A. Koch en alguna parte del trabajo algorítmico.
Si la conjetura de los cuatro colores fuera falsa, habría al menos un mapa con el menor número posible de regiones que requiere cinco colores. La demostración muestra que este contraejemplo mínimo no puede existir, a través del uso de dos conceptos técnicos:
- Un conjunto inevitable es un conjunto de configuraciones tales que cada mapa debe tener al menos una configuración de este conjunto.
- Una configuración reducible es una disposición de países que no puede ocurrir en un contraejemplo mínimo. Si un mapa contiene una configuración reducible, entonces el mapa se puede reducir a un mapa más pequeño. Este mapa más pequeño tiene la condición de que si se puede colorear con cuatro colores, entonces el mapa original también puede. Esto implica que si el mapa original no se puede colorear con cuatro colores entonces el mapa más pequeño tampoco puede, por lo que el mapa original no es mínimo.
Utilizando reglas y procedimientos matemáticos basados en las propiedades de las configuraciones reducibles, Appel y Haken encontraron un conjunto inevitable de configuraciones reducibles, y demostraron por tanto que no podía existir un contraejemplo mínimo para la conjetura de los cuatro colores. Su demostración redujo la infinitud de posibles mapas a 1.936 configuraciones reducibles (posteriormente fueron reducidos a 1.476), que tuvieron que ser comprobadas una por una por ordenador, lo que duró más de mil horas. Esta parte sobre la reductibilidad del trabajo fue comprobada independientemente con programas y ordenadores diferentes. Sin embargo, la parte de inevitabilidad de la demostración se verificó en más de 400 páginas de microfilm , que tuvieron que ser comprobadas a mano.
Los medios de comunicación de todo el mundo difundieron ampliamente el anuncio de Appel y Haken, y el departamento de matemáticas de la Universidad de Illinois utilizó un matasellos que decía "Con cuatro colores basta" . Asimismo, el carácter inusual de la demostración -fue el primer teorema importante que se demostró con una amplia asistencia del ordenador- y la complejidad de la parte verificable por humanos despertó una gran controversia.
A principios de la década de 1980, se difundieron rumores de un error en la demostración de Appel-Haken. Ulrich Schmidt, de la Universidad Técnica de Aquisgrán, examinó la demostración de Appel y Haken como tema de su tesis de máster. Había comprobado un 40% de la parte sobre la inevitabilidad y había encontrado un error significativo en el procedimiento de descarga. En 1986, el editor de la revista The Mathematical Intelligencerpidió a Appel y Haken que escribieran un artículo sobre los rumores de errores en su demostración. Ellos respondieron que los rumores eran causados por una "mala interpretación de los resultados [de Schmidt]" y correspondieron con un detallado artículo. Su obra magna, Todos los mapas planares son 4-acoloribles (inglés: Every Planar Map is Four-coloreable ), un libro que alegaba contener una demostración completa y detallada (con un suplemento de microfilm de más de 400 páginas), apareció en 1989 y contaba el descubrimiento de Schmidt y varios errores adicionales encontrados por otros.
Simplificación y verificación
Desde la demostración del teorema, se han encontrado algoritmos eficientes que colorean mapas con 4 colores y requieren sólo un tiempo O ( n 2 ), donde n es el número de vértices. En 1996, Neil Robertson, Daniel P. Sanders, Paul Seymour y Robin Thomas crearon un algoritmo de tiempo cuadrático, mejorando un algoritmo QuarTIC basado en la demostración de Appel y Haken. Esta nueva demostración es similar a la de Appel y Haken pero más eficiente, ya que reduce la complejidad del problema y requiere la comprobación de sólo 633 configuraciones reducibles. Tanto las partes de inevitabilidad como de reducibilidad de esta nueva prueba deben ser ejecutadas por ordenador y no es factible comprobar a mano. En 2001, los mismos autores anunciaron una demostración alternativa, en demostrar el teorema del Snark.
En 2005, Benjamin Werner y Georges Gonthier formalizaron una demostración del teorema dentro del asistente de pruebas Coq . Esto elimina la necesidad de confiar en los diversos programas de ordenador utilizados para verificar los casos particulares; sólo hay que confiar en el núcleo de Coq.
Resumen de las ideas de la demostración
Alfred Kempe
La siguiente discusión es un resumen basado en la introducción del libro de Appel y Haken Todos los mapas planos son 4-acoloribles (inglés: Every Planar Map is Four coloreable ). Aunque con errores, la supuesta demostración original de Kempe del teorema de los cuatro colores proporcionó algunas de las herramientas básicas utilizadas más tarde para demostrarlo. La explicación de esta sección se ha reformulado en términos de la teoría de grafos moderna.
El argumento de Kempe es el siguiente. En primer lugar, si las regiones planas separadas por grafo no están trianguladas (es decir, no tienen exactamente tres aristas en sus límites), podemos añadir aristas sin introducir nuevos vértices y hacer que cada región sea triangular, incluida la región externa. Si este grafo triangular es acolorible con cuatro colores o menos, también lo es el grafo original, ya que el mismo coloreado es válido si se eliminan las aristas que se habían añadido. Así que para demostrar el teorema de los cuatro colores para todos los grafos planos es suficiente demostrarlo para grafos triangulados, y sin pérdida de generalidad podemos asumir que el grafo es triangulado.
Supongamos que v , a , y c son el número de vértices, aristas y regiones (caras). Dado que cada región es triangular y cada arista es compartida por dos regiones, encontramos que 2 a = 3 c . Esto, junto con la relación de Euler v - a + c = 2, se puede utilizar para demostrar que 6 v - 2 a = 12. Ahora, el grado de un vértice es el número de aristas que inciden. Si v n es el número de vértices de grado n y D es el grado máximo de cualquier vértice, entonces
Pero como 12> 0 y 6 - y ≤ 0 para todo y ≥ 6, esto demuestra que hay al menos un vértice de grado 5 o menos.
Si hay un grafo que requiere 5 colores, entonces hay un grafo mínimo que requiere 5 colores, como la eliminación de cualquiera de sus vértices hace que sea de 4-acolorible. Llamamos este grafo G . G no puede tener un vértice de grado 3 o menos, porque si de ( v ) ≤ 3, entonces podríamos eliminar v de G , colorear el nuevo grafo con cuatro colores, y luego añadir de nuevo v y ampliar el coloreado con 4 colores el grafo original escogiendo para v un color diferente al de sus vecinos.
Kempe también demostró correctamente que G no puede tener ningún vértice de grado 4. Al igual que antes, eliminamos el vértice v y acolirim los vértices restantes con cuatro colores. Si los cuatro vecinos de v son de diferentes colores, por ejemplo rojo, verde, azul y amarillo en sentido horario, buscamos una ruta alterna de vértices de color rojo y azul que unan los vecinos rojo y azul. Este camino se llama una cadena de Kempe. Puede haber una cadena de Kempe que una los vecinos rojo y azul, y puede haber una cadena de Kempe que una los vecinos verde y amarillo, pero no pueden existir las dos cadenas simultáneamente, ya que estos dos caminos deberían cruzar necesariamente, y el vértice donde se cruzan no se podría colorear. Supongamos que son los vecinos rojo y azul que no están encadenados entre sí. Exploramos todos los vértices conectados al vecino rojo por caminos alternos rojo-azul y, a continuación, invertimos los colores rojo y azul en todos estos vértices. El resultado sigue siendo una coloración de cuatro colores válida, y ahora podemos añadir v de nuevo y colorearlo de color rojo.
Esto deja sólo el caso en que G tiene un vértice de grado 5; pero la argumentación de Kempe era defectuosa en este caso. Heawood se dio cuenta del error de Kempe y también observó que el método sí servía para demostrar que con cinco colores basta. En efecto, siguiendo la argumentación anterior (cambiando sólo que el contraejemplo mínimo necesita 6 colores) y utilizando cadenas de Kempe en la situación de un vértice de grado 5, se puede demostrar el teorema de los cinco colores .
En cualquier caso, para hacer frente a este caso de un vértice de grado 5 hay una noción más complicada que la simple eliminación de un vértice. Más bien, la forma del argumento se generaliza considerando configuraciones , que son subgrafos de G conexos con el grado de cada vértice (en G ) especificado. Por ejemplo, el caso descrito en la situación del vértice de grado 4 es la configuración que consta de un solo vértice etiquetado como grado 4 en G. Como antes, es suficiente demostrar que si se elimina la configuración y el grafo restante es 4-acolorible, entonces se puede modificar la coloración de tal manera que cuando se vuelve a añadir la configuración la 4-coloración puede extenderse también al grafo G . Una configuración por la que esto es posible se denomina una configuración reducible . Si de un conjunto de configuraciones hay al menos una que debe ocurrir forzosamente en algún lugar de G , este conjunto se denomina inevitable . El argumento anterior comenzó dando un conjunto inevitable de cinco configuraciones (un solo vértice con grado 1, un solo vértice con grado 2, ..., un solo vértice con grado 5) y después se procedió a demostrar que los primeros 4 son reducibles; mostrar un conjunto inevitable de configuraciones en el que todas las configuraciones son reducibles equivaldría a demostrar el teorema.
Como G es triangular, se conoce el grado de cada vértice en una determinada configuración, y se conocen también todas las aristas internas de la configuración, el número de vértices de G adyacentes a una configuración dada es fijo, y están unidos en un ciclo . Estos vértices forman el anillo de la configuración; una configuración con un anillo de k vértices es una configuración de k-anillo, y la configuración junto con el anillo se denomina configuración anillada . Como en los casos anteriormente indicados, se pueden enumerar todas las diferentes 4-coloraciones del anillo; cualquier coloración que se pueda extender sin modificación a una coloración de la configuración se denomina inicialmente buena . Por ejemplo, la configuración anterior de un solo vértice con 3 o menos vecinos era inicialmente buena. En general, el grafo que la rodea debe ser sistemáticamente reacolorit para convertir la coloración del anillo en una coloración buena, como en el caso anterior de 4 vecinos; en una configuración general con un anillo más grande, esto requiere técnicas más complejas. Debido a la gran cantidad de 4-coloraciones diferentes del anillo, este es el paso principal que requiere ayuda del ordenador.
Finalmente, queda por identificar un conjunto inevitable de configuraciones susceptibles de reducción con este procedimiento. El principal método utilizado para descubrir un conjunto de este tipo es el método de descarga. La idea intuitiva subyacente al método de descarga consiste en considerar el grafo plano como una red eléctrica. Inicialmente, se distribuye una "carga eléctrica" entre los vértices de tal manera que el total sea positivo.
Recordemos la fórmula anterior:
En cada vértice se le asigna una carga inicial de 6 - d ( v ). Entonces, se hace "fluir" la carga a través de redistribuirla sistemáticamente desde un vértice a sus vértices vecinos de acuerdo con un conjunto de normas: el procedimiento de descarga . Dado que la carga se conserva, algunos vértices siguen teniendo carga positiva. Las normas restringen las posibilidades de configuraciones de vértices con carga positiva, por lo que la enumeración de todas estas configuraciones posibles da un conjunto inevitable.
Mientras algún elemento del conjunto inevitable no sea reducible, se modifica el procedimiento de descarga con el fin de eliminarlo (a la vez que se introducen otras configuraciones). El procedimiento de descarga final de Appel y Haken tenía una gran complejidad y, junto con una descripción del conjunto de configuraciones inevitable resultante, llenaba un volumen de 400 páginas, pero se podía comprobar mecánicamente que las configuraciones que generaba eran reducibles. La verificación por expertos del volumen que describe el conjunto de configuraciones inevitable duró varios años.
Un detalle técnico que no se ha discutido aquí, pero que se necesita para completar la demostración, es la reductibilidad de inmersión .
Refutaciones falsas
El teorema de los cuatro colores ha atraído un gran número de demostraciones y refutaciones falsas en su larga historia. Inicialmente, The New York Times se negó a informar sobre la demostración de Appel-Haken por temor a que la demostración resultase falsa como las anteriores. Algunas supuestas demostraciones, como la de Kempe y la de Tait mencionadas anteriormente, estuvieron bajo el escrutinio público durante más de una década antes de ser expuestas. Pero muchas más, escritas por aficionados, ni siquiera se llegaron a publicar nunca.
En general, los contraejemplos más simples (aunque inválidos) intentan crear una región que toque todas las demás regiones. Esto fuerza que las otras regiones deban colorear con sólo tres colores. Como el teorema de los cuatro colores es cierto, esto siempre es posible; sin embargo, como la persona que dibuja el mapa se centra en la región grande, no se da cuenta que las regiones restantes se pueden de hecho colorear con tres colores.
Este truco se puede generalizar: hay muchos mapas en los que si se seleccionan los colores de algunas regiones de antemano, se hace imposible colorear las otras regiones sin exceder los cuatro colores. Un verificador casual del contraejemplo puede no pensar en cambiar los colores de estas regiones, por lo que el contraejemplo aparecerá como válido.
Quizás uno de los efectos que subyace a este error común es el hecho de que la restricción de color no es transitiva : una región sólo se debe colorear de un color diferente de las regiones que toca directamente, no de las regiones que tocan las regiones que la primera toca. Si esta fuera la restricción, los grafos planos requerirían un número arbitrariamente grande de colores.
Otros refutaciones falsas violan los supuestos del teorema de maneras inesperadas, tales como el uso de una región que consiste en múltiples partes desconectadas, o prohibiendo regiones del mismo color que se toquen en un punto.
Generalizaciones
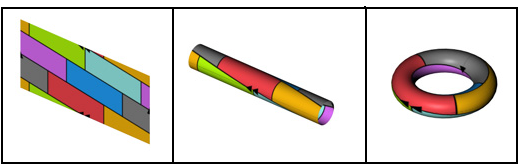
Al unirse las flechas individuales entre ellas y las flechas dobles entre ellas, se obtiene un torre con siete regiones que se tocan mutuamente; por lo tanto, son necesarios siete colores.
Esta construcción muestra el toro dividido en un máximo de siete regiones, cada una de las cuales toca todas las demás.
El teorema de los cuatro colores se aplica no sólo a grafos planos finitos, sino también a grafos infinitos que se pueden dibujar sin cruzarse en el plan, y de manera aún más general, a grafos infinitos (posiblemente con un número incontable de vértices ) para los que cada subgrafo finito es plano. Para demostrar esto, se puede combinar la demostración del teorema para grafos planos finitos con el teorema de De Bruijn-Erdős , que dice que si cada subgrafo finito de un grafo infinito es k -acolorible, entonces todo el grafo es también k - acolorible. Esto se puede ver también como una consecuencia inmediata del teorema de compacidad de Kurt Gödel en Lógica de primer orden , expresando la coloración de un grafo infinito como un conjunto de fórmulas lógicas.
Se puede considerar también el problema de coloración en superficies que no sean el plan. El problema en la esfera o el cilindro es equivalente al del plan. Para superficies cerradas (orientables o no) con género positivo, el número p máximo de colores necesarios depende de la característica de Euler χ de la superficie de acuerdo con la fórmula
donde las claves exteriores denotan la parte entera.
Alternativamente, para una superficie orientable la fórmula se puede expresar en términos del género de una superficie, g :
Esta fórmula, llamada la conjetura de Heawood , fue conjeturada por Pearcy John Heawood en 1890 y demostrada por Gerhard Ringel y JTW Youngs en 1968. La única excepción a la fórmula es la botella de Klein , que tiene característica de Euler 0 (y por tanto la fórmula da p = 7) y requiere 6 colores, como demostró P. Franklin en 1934.
Por ejemplo, el tor tiene característica de Euler χ = 0 (y género g = 1) y por lo tanto p = 7, así que se necesitan como máximo 7 colores para colorear cualquier mapa en un toro. El poliedro de Szilassi es un ejemplo que necesita siete colores.
Una cinta de Möbius necesita seis colores,así como los grafos 1-planos (grafos dibujados con un cruce sencillo para corte como máximo). Si se colorean tanto los vértices como las caras de un grafo plano, de modo que no hay dos vértices adyacentes, caras, o pares de vértices y caras que tengan el mismo color, se necesitan de nuevo un máximo de seis colores.
Ninguna extensión obvia del resultado de coloración por regiones sólidas tridimensionales. Mediante el uso de un conjunto de n varillas flexibles, se puede hacer que cada varilla toque las otras varillas. El conjunto requeriría entonces n colores, o n +1 si se tiene en cuenta el espacio vacío que también toca a cada varilla. El número npuede ser un entero tan grande como se quiera. Fredrick Guthrie conocía ya estos ejemplos en 1880. Incluso para cuboides de ejes paralelos (que se consideran adyacentes cuando dos cuboides comparten un área límite de dos dimensiones) pueden necesitar un número ilimitado de colores.